An Introduction to Fundamental Research on the Mechanism of the Electrodeposition of Metals

 

 

by

Brian E. Conway, University of Ottawa

Ottawa, Ontario, Canada

and

John O’Mara Bockris, University of Pennsylvania

Philadelphia, Pennsylvania, USA

Technical Editor’s Note: From time to time, it has been our intent to present seminal papers from past issues of NASF/AESF journals that are of such significance that, decades later, they bear another look.  It is hoped that our rich and illustrious heritage might inspire others to reinvigorate the technological prowess of our industry.

This paper last ran in the AESF Journal of Applied Surface Finishing in 2007 [JASF, 2 (4), 257-272 (2007)], and was part of AES Research Project No. 16 and originally published as AES Research Serial Report No. 41, after publication in the AES journal [Plating, 46, 371-83 (1959)].

As Einstein is associated with relativity, Drs. Conway and Bockris are synonymous with theoretical electrochemistry, and the AES was privileged to have their services in the form of AES Research Project #16, entitled “Mechanism of Electrodeposition.”  This project studied the various steps involved in the electrodeposition and electrocrystallization of a metal.  Part I of the project included short time polarization measurements while a monatomic layer of metal was deposited.  It was concluded that electrodeposition involved the transfer of a metal ion through the electrode double layer to the cathode surface.  Part II examined planes of a copper single crystal, concluding that macrosteps were caused by misorientations of the surface.  This paper is in large measure, the result of Project #16, and, as the authors modestly describe it, is “an attempt to describe to the electroplater who understands the basic ideas of electrochemistry, what is being done in research on fundamental electrode processes.”  This “attempt” did rather well.  A printable version of this paper is available by clicking HERE.

ABSTRACT

An attempt is made to explain the type of work done in fundamental research on the mechanism of metal deposition.  The object is to ascertain: (a) the structure of the electric double-layer, (b) the structure of ions in solution which give rise to electrodeposited entities, (c) the path and rate-determining step in the metal deposition.  An explanation of the technical terminology of the work is given in an Appendix.  Particular techniques, especially pre-electrolysis, and the introduction of clean surfaces into the solution, are discussed.  Some experimental results of one fundamental investigation on the AC impedance of the copper solution interface are given.  The interpretation of these results is briefly discussed.  They are consistent with the view that the transfer of ions is largely rate-determining except near the reversible potential.  It is also possible to make a purely theoretical approach to metal deposition kinetics and the type of result ensuing from this is described.

I. Introduction

This paper represents an attempt to describe to the electroplater who understands the basic ideas of electrochemistry, what is being done in research on fundamental electrode processes, and in particular how electrochemical workers are tackling the problem of finding out the sequence and nature of the ionic and molecular events which occur during electroplating.  One value of such work is as a foundation on which substantial advances in practical electrodeposition can be made.

Accordingly, problems which are the object of research in fundamental work on electrodeposition are described.  Some typical experimental techniques which have been used in fundamental work are then presented, and a brief outline is given of how one particular piece of experimental research was carried out.  Some terminology and ideas which fundamental electrochemists use in discussing the mechanism of electrodeposition are informally defined.  Finally, a summary is given of how evidence concerning the rate-determining step in a typical simple metal deposition reaction has been obtained in recent fundamental research carried out at the University of Pennsylvania and the University of Ottawa as part of AES Research Project No. 16.  It is shown how not only fundamental experimental work, but also purely theoretical considerations, can contribute to the evaluation of the detailed molecular mechanism of metal deposition.

Practical work is being served by this research.  Electroplating as it is generally practiced has "just grown."  The basic mechanisms are little understood, since the theory of electrode kinetics has existed in any depth for only some ten years.  This article is an attempt to bridge the wide gap between practice and theory in the metal deposition industry.

II. Typical problems chosen as the subjects of fundamental work in metal deposition

Since the basic problem in metal deposition is the discovery of the molecular mechanism which occurs when a metal ion is deposited electrochemically on a metal of the same species, the following are the three general questions to be answered in order to obtain complete understanding of metal deposition.

(1) What is the structure of the electric double layer at the metal /solution interface?

At the present time, only the structure of the mercury/solution interface is known in detail.¹  The "structure of the interface" means how the ions together with their hydration sheaths (Fig. 1) on the solution side of the double layer and how the electrons on the metal side of the double layer are arranged as a function of distance from the metal-solution boundary.  In what way, and at what concentration, are the solvent molecules arranged at the interface?  (In particular, with positive ends of the dipoles inwards or outwards?)  Are the anions of the electrolyte simply distributed in the electrostatic field near to the electrode, or are they attached to the electrode by chemical binding forces of a non-coulombic nature?  What is the strength of any of the metal-ion or metal-solvent molecule bonds formed? (Correspondingly, how much work does an ion which is approaching the electrode have to do in displacing one of the adsorbed particles on the electrode so that it can find a place for itself?)  How do the quantities mentioned above depend upon temperature, concentration and composition of the solution?  With what kind of bond and with what bond strength are additives adsorbed on the electrode?  What are the contours of the basis metal before deposition begins?  What is the ratio of true to apparent surface areas on the metal and how is this influenced by the adsorption of solvent, anions and additives?  What is the magnitude of the potential difference at the metal-solution interface created by the layer of adsorbed solvent molecules?

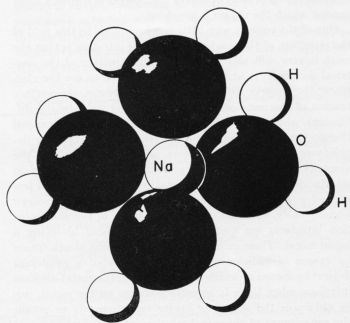
Figure 1 - Sodium ion with hydration sheath containing four water molecules.

Such questions concerning the structure of the double-layer exemplify the kinds of information which the fundamental chemist must try to obtain before he tackles the central problem of the mechanism of electrodeposition.  Without such knowledge, particularly that concerning the amounts of adsorbed molecules attached to the electrode, he is limited in what he can do in evaluating mechanisms, because he is not sure what is on the electrode surface.  He is like somebody attempting to ascertain the path of the movement of another person in a dark room by the sounds he hears, when he does not know the objects in the dark room against which the person is knocking.

One of the reasons why little has been done in this field of the structure of the solid-metal-solution interface is that the work is very difficult.  In work on the structure of the electrical double-layer at mercury, it is possible to use the electrocapillary curve (i.e., the relation between the surface tension of the metal-solution interface and its potential difference), which allows the application of some rather general thermodynamic reasoning to the relations between the dependence of the surface tension on concentration and the amounts of adsorbed material present.^2,3  The metal-solution interfacial tension when the metal is a solid is a much less accessible experimental quantity than it is with mercury.⁴  Consequently, methods used for the study of the solid-solution interfaces are quite different from those involving a liquid metal.  These include direct measurement of adsorption by means of radioactive tracers;⁴ the use of a pendulum device⁵ by means of which the potential of the metal-solution interface, when there is no surface charge on the metal, can be obtained; the use of AC bridge measurements to obtain the capacitance of the metal-solution interface,⁶ which may, in the presence of certain supporting information, be made to yield the amounts of the various constituents adsorbed at the interface (Fig. 2); and finally, direct spectrophotometric determination.⁷

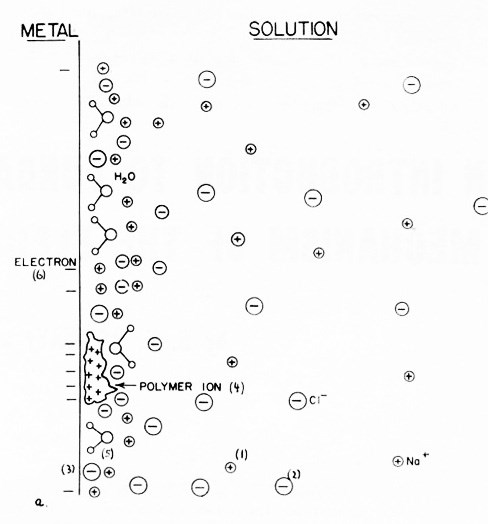
(a)

(b)

Figure 2 - (a) The distribution of ions and dipoles in the electrical double-layer: (1) cations, (2) anions, (3) specifically adsorbed anions, (4) adsorbed additives, (5) adsorbed water dipoles, (6) electrons.  (b) The potential as a function of distance in the double layer (corresponding to (a)), measured from the metal surface.

(2) What is the constitution of the ions in the solution which are the source of the electrodeposited entity?

It is obvious that there are "two sides" to the problem of metal deposition mechanisms: the electrode and the solution side.  The essence of the problem in the latter case is knowledge of the constitution of the ions which yield the metal atom which is deposited.  This problem may be subdivided into two parts.

In very simple solutions of ions which do not usually form complexes, for example, in an acidified CuSO₄ solution, the nature of the depositing ion is always obvious, e.g., Cu⁺⁺.  However, there is still the problem of the constitution of the hydration sheath of such an ion, namely, its shape and size in pure aqueous solutions and its composition if organic molecules are present to share it with the water.  This is certainly a question of enormous importance which is tacitly avoided in many discussions because we usually write equations for electrode reactions without mentioning the solvation sheath.  It is just this environment which is responsible for many of the differences between aqueous, non-aqueous and molten salt deposition - and so it must be better understood, if the ionic mechanism of deposition is to be elucidated in a given system.

Determination of the constitution of a solvation sheath, e.g., for Na⁺ (Fig. 1), has recently become moderately well understood.⁸  However, the methods which are now available have been applied almost exclusively to the alkali and alkaline-earth metal ions,⁹ and there is a considerable deficiency in our knowledge of the solvational properties of those metal ions which are of interest in technical plating processes.  Correspondingly, difficulties exist in the evaluation of deposition mechanisms involving such ions in practical systems.

In many, perhaps most, technically important solutions, the ions which electrodeposit are not simple.  They are complex ions, sometimes anionic.  A classic example is the complex formed when KCN is added to a solution of a silver salt.  A complex ion |Ag(CN)₂]^– is formed and the deposition of silver can occur from such solutions of this anion.*

Knowledge of complex ions in aqueous solutions is relatively good, although little is known of their behavior in solutions as modified for plating practices, e.g., at elevated temperatures or in the presence of organic substances.  However, an almost complete lack of knowledge exists in the case of non-aqueous solvents (where a good deal of the future of plating processes may lie) or in molten salts, where explicit methods of evaluating the constitution of complex ions have been obtained only in recent months,¹⁰ and very few results are as yet available.**

(3) What is the mechanism?

The central questions which the fundamental research worker asks about an actual deposition process itself (having discovered, as indicated above, the constitution of entities in the solution comprising the ion, and the structure of the double-layer, through which the depositing entity has to pass) are these:

(i)         What is the overall reaction?

(ii)         What is the path of the reaction?

(iii)        What is the rate-determining reaction among the several consecutive reactions which make up this path?

(i) The overall reaction: For the example chosen, this is obviously:

Cu⁺² + 2e^– ↔ Cu

If the overall reaction is not obvious, it can be found by classical types of experiments in which the potential of the electrode is measured as a function of the activity of the ions in the solution.  The appropriate form of the logarithmic relation between potential and the "activity fraction," i.e., "mass action fraction," of the reactants and products in the overall reaction is then found.  As this depends characteristically upon the cell reaction, the latter thereby becomes determined.

(ii) The path of the reaction: There are usually several paths to be discussed.  Two hypothetical and illustrative paths are given in Table 1.

Table 1 - Hypothetical reaction paths.

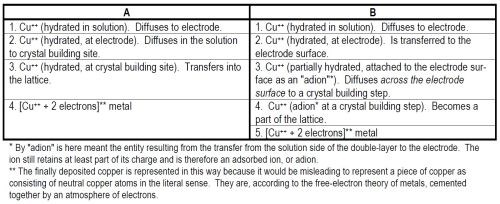
(iii) The rate-determining step:  Electrode reactions, like many chemical reactions, consist for a given typical ion, of a series of consecutive reactions, as illustrated in A and B in Table 1.***  In any such series, there is nearly always one reaction the rate of which is the bottle-neck for the whole process, i.e., the rate which controls the rate of the overall process of deposition, and consequently is called the rate-determining step (Fig. 3).  The concept of the rate-determining step is the central concept in electrode kinetics.  The fundamental research worker regards a knowledge of the rate-determining step in the metal-deposition reaction as the key question, to the solution of which all other investigations are complementary.  The central importance of the rate-determining step over all other matters to be investigated in an electrode reaction depends upon the fact that the kinetic behavior of the overall reaction depends on the one rate-determining reaction in every way - other steps have little influence.  The rate-determining step is to the overall reaction rate what an overwhelmingly big series resistance is to the current in an electrical circuit containing in addition several other small resistances in series with the large one.  To some extent, therefore, the question of the mechanism of an electrodeposition reaction comes down essentially to the one question: What is the rate-determining step?

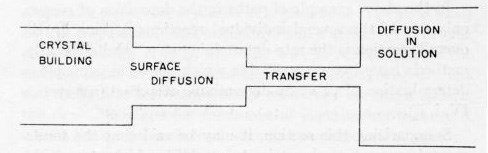
Figure 3 - As in a series of tubes the one with the smallest diameter determines the overall flow of liquid, in a series of consecutive reactions the one with the highest activation energy determines the overall rate of the process.  In the diagram this corresponds to the narrow channel called ion "transfer."

In the above example of paths in the deposition of copper, only one of the several individual reactions making up the overall reaction is the rate-determining step.  Quite recently, methods have become available which allow, in principle, a determination of this rate-determining step.^13,14 (see section IV, parts 1, 2).

Summarizing this section, it may be said that the fundamental research worker tries to establish which atoms, ions and molecules exist at the beginning and end of the process of deposition.  He then lets the deposition process occur (at first under the simplest controlled conditions he can devise) and measures quantities which will give him evidence concerning which, of a number of possible consecutive reactions, controls the rate of the overall metal-deposition process.  These consecutive steps together constitute the "mechanism of deposition," concealed, as it were, in the non-descriptive "overall reaction" or stoichiometric equation as usually written to represent the process.

III. Experimental techniques

Differences in experimental techniques used in fundamental work and those used in practical plating processes are extreme and originate in the following way.  The practical plater is interested in bringing about a combination of many complex circumstances which he finds by experience give him practically useful metallic deposits.  The fundamental chemist is interested in breaking the process down to its very essentials, and to do this he has to aim, until he has understood these essentials, at the very simplest possible conditions.  He will never find out the mechanism which gives rise to a bright nickel plate from a Watts type bath if he has not discovered the bricks and mortar of the process - the deposition of nickel from a very simple solution, first; and consequently, unless he has completed these basic studies, there is little prospect of fundamental researches reaching a stage where they can be helpful to practical workers.

This attitude gives rise to emphasis on technique in which as many variables as possible are controlled.  Two examples of such techniques will be given.

(i) The purification of solutions.  The remarkable sensitivity to impurities of electrode reactions in general, particularly at solid-solution interfaces, has been known for only a comparatively short time, and methods for preparing solutions in such a way that the effects of trace impurities in them are reduced to a level where they are no longer effective are relatively new.¹⁵ †  Impurities complicate the mechanism of an electrode reaction in two ways.  Firstly, the impurities may themselves set up electrode reactions so that the potential and current measured in an experiment are not simply concerned with the intended reaction, but are complex mixed potentials and current densities, and hence useless from the point of view of getting fundamental information.  Depolarization of the electrodeposition of hydrogen by oxygen is the best known of such processes,¹⁸ and was one of the causes of the great difficulty experienced for many years in determining hydrogen over-potential at low current densities.

Secondly, some impurities adsorb on the electrode and therefore change the composition and structure of the double-layer.  Consideration of this effect shows that a high degree of purification of solutions from adsorbable trace impurities is necessary in order that an electrode reaction may be studied without complicating side effects.  Thus, these impurities in a solution do not necessarily remain homogeneously distributed in this solution, but often concentrate at interfaces.  In effect, they therefore become preferentially concentrated either on the glass of the cell or on the electrode and certainly with some impurities the adsorption will be preferentially upon the metal electrode.  Further, the surface of the electrode is certainly not generally homogeneous and has some areas more likely to adsorb materials than others.  To obtain a rough idea of the order of the minimum concentration of impurities which has to be feared, let us assume that all of some particular impurity present in the compartment of an experimental cell (the cell used in this work is shown in Fig. 5) is adsorbed on an electrode of area 1 cm² and that an effect on the electrode process is noticeable when one-tenth of the apparent surface area of the electrode is covered.  Now, since about 3×10^-7 grams of a small sized molecule (e.g., H₂S, As₂O₃, etc.) is sufficient to cover 1 cm² of an electrode, we have to fear 3×10^-8 grams of impurity in the cell solution.  A typical experimental cell may have 100 mL of solution in the compartment containing the electrode, so that, with our present assumptions, this 100 mL must contain less than 3×10^-8 grams of impurity, i.e., less than one three-thousandth of a part per million.  Measurable effects caused by traces of this order have indeed been detected.¹⁵

There is no chance of purifying solutions to this degree by normal chemical methods such as distillation or recrystallization, although these methods must clearly be used in the initial stages of purification.  Pre-electrolysis†† has been found to be the most useful method.  The technique of this method consists of (a) inserting a scavenger (or dummy) electrode into the solution in which the fundamental measurements are to be carried out, (b) allowing electrolysis on one or more scavenger electrodes to occur for a period, determined by experiments, such that no further change occurs in the experimental results if the time of pre-electrolysis is further increased, (c) removing the scavenger electrode from the solution and inserting a test electrode.  The period of pre-electrolysis depends upon the detailed conditions of the experiment, the concentration of the solution, type of salts, etc.  A typical condition would be that pre-electrolysis is carried out at a current density of 10 amp/ft² for 24 hr in a volume of solution about 150 mL on an electrode 1 cm² in area.

Pre-electrolysis purification is not used exclusively to eliminate interference in electrode reactions by trace impurities.  Other methods, e.g., adsorption on sheets of palladized asbestos,²² may be helpful.  The importance of pre-electrolysis is in removing very small traces, after other methods of purification have removed grosser quantities.

(ii) The preparation of electrodes.  The type of surface (planes with particular orientation, single crystals, poly-crystals, etc.) of the metal used in a metal deposition process is clearly of importance.  More important, however, is the fact that this surface should be reproducible and free from contaminants having the nature of metal oxides, organic fats or greases, etc.  This is very difficult to achieve by any method in which the electrode surface is allowed to come into contact with air before insertion into the test solution (which also must not at any time be in contact with air) because of the fact that ordinary air has sufficient impurities to cover any electrode exposed to it with a film within a few seconds.²³  It is not usually satisfactory to rely upon purification of the electrode within the cell, because of the complex changes of solution and the consequent repurification which would then be necessary.

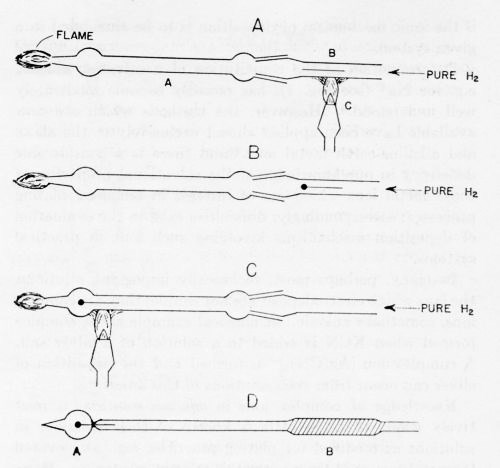
Figure 4 - Electrode preparation: A Pyrex tube A is connected with a quartz tube B; a copper wire is heated in an H₂-atmosphere until one end fuses into a sphere.  The electrode is then sealed into the glass tube as in C and D.

In a method¹⁹ which avoids these difficulties, a spectroscopically pure wire is placed in a glass tube (the glass must be free from arsenic and antimony) and a stream of hydrogen passed through it (Fig. 4).  The wire is heated just to the melting point in a stream of highly purified hydrogen.  The end melts first and immediately rolls itself up into a sphere, the desirable shape for fundamental experiments because it avoids the special surface conditions associated with "points."  After passage of hydrogen for a time and at a temperature sufficient to create a perfectly clean surface (manifested in most metals by specular appearance under a microscope), the bulb is sealed.  The electrode is then ready for use.  The glass tube to which it is attached may be inserted into a ground glass tube at the top of the cap of the cell and then the cap inserted into the cell before final washing of the interior of the cell.  During these operations, neither the electrode nor the holder nor any part of the electrode arrangement is touched by hand - a liberal purveyor of organic impurities.  They are handled only by very well cleaned platinum-tipped forceps.  After the tube is inside the cell, and much later, after the solution has been prepared, pre-electrolyzed, etc., the thin glass bulb around the spherical electrode is easily shattered by means of a plunger inside the cell and experiments made upon the spherical electrode, which has thus been brought into contact, without contamination, with the highly purified solution.  These examples of technique in fundamental work illustrate the complications needed for simplicity and good definition of the final system.

IV. Some experimental aspects of a recent fundamental study

In recent work by the authors on the mechanism of the exchange reaction between copper and acid copper sulfate solution, the measuring cell was as shown in Fig. 5.  The glass barrels holding the electrodes were moistened with solution and held in position by metal clips.  Grease was rigorously excluded from the cell.  Four test electrodes were in the cell, a fifth served for pre-electrolysis and a sixth consisted of a cylindrical platinum gauze of large area into the center of which the test electrodes could be positioned.  A low amplitude AC signal was applied between the test electrode and the gauze electrode, which served to form one arm of an AC Wheatstone bridge, thus enabling resistance and capacitance of the cell to be measured.  (The fact that the counter-electrode has a very large area and the test electrode a very small one means that in measuring the capacity and resistance of the cell one is, in effect, measuring the small electrode.)

Figure 5 - Cell for measurements with highly purified solutions.  The central compartment contains the test electrodes of copper.  The right-hand compartment contains an anode for passing a current between it and the copper electrode.  The left hand compartment contains a reference electrode for potential measurements.

In the investigation cited, most work was carried out with 0.01 to 100 g/L CuSO₄ in H₂SO₄ (10%).  The cell was cleaned before and after each run with nitric-sulfuric acid mixture and washed with distilled water and equilibrium water (ϰ = 10^-6 mho/cm) only.  The latter was distilled in helium before entry into the cell and then had ϰ = 3 × 10^-7 mho/cm.  For experiments in which sulfuric acid was used, arsenic-free analytical grade sulfuric acid was distilled in vacuo in an all-glass apparatus and transferred to the cell in a calibrated transfer pipette closed to the atmosphere.  The amount required to give a desired acid concentration was then added to water distilled into the cell through a side arm.  CuSO₄ crystals (99.99% CuSO₄∙5H₂O) were recrystallized twice from conductance water outside the cell and twice more in closed flasks under helium, connected with an auxiliary cell containing two copper cathodes, and an anode of Pt, which permitted pre-electrolytic purification of the recrystallized, saturated CuSO₄ solution before its introduction into the sulfuric acid solution, which had been previously purified in the main cell by means of pre-electrolysis.

Electrodes were prepared as described above.

The bridge was essentially a simple AC bridge.  It contained an oscillator with a range from 5 to 5×10⁵ Hz.  To amplify the balanced voltage of the bridge, a symmetrical amplifier was introduced between the bridge and the signal amplifier (a Hewlett-Packard wave-analyzer).  Such a bridge is not easy to operate satisfactorily in the absence of a wave-analyzer, because the amplitude of the applied signal is low (5 mV) and balance is difficult to achieve in the presence of a normal amount of noise.

(1) Example of the investigation of the electrode impedance for a copper electrode in a solution of CuSO₄

In this work the aim is to evaluate the rate of deposition of copper ions across the double-layer.  This may be achieved by determining the impedance offered by the electrode-solution system to an applied AC.  This impedance is however complex, containing effectively ohmic and capacitative components, corresponding to processes involved in the transfer of the ions from the solution to the electrode.  Its behavior with regard to admittance of the alternating current at various frequencies can best be understood in terms of the simplest network of resistances and capacitances which can be devised, which gives an impedance having the same characteristics as that of the electrode-solution interface.  A certain model or "equivalent circuit" (see VII) is set up experimentally (Fig. 6) and the values of the ohmic (R_E, R_L in Fig. 6) capacitative (C_L in Fig. 6) components involved are then evaluated from experimental measurements, using an applied AC at various frequencies.

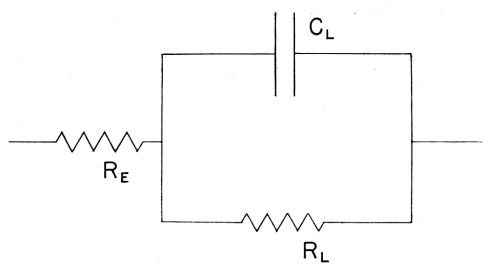
Figure 6 - The equivalent circuit for the electrolytic cell; R_E = electrolytic resistance; R_L = electrode resistance; C_L = electrode capacitance.

(i) Some experimental results in this system.  Electrode capacitance measurements in the absence of CuSO₄ in solution, and in the range of potentials where no copper dissolves in the solution and no hydrogen is evolved, give values of about 70 μF per apparent cm² of electrode area.†††

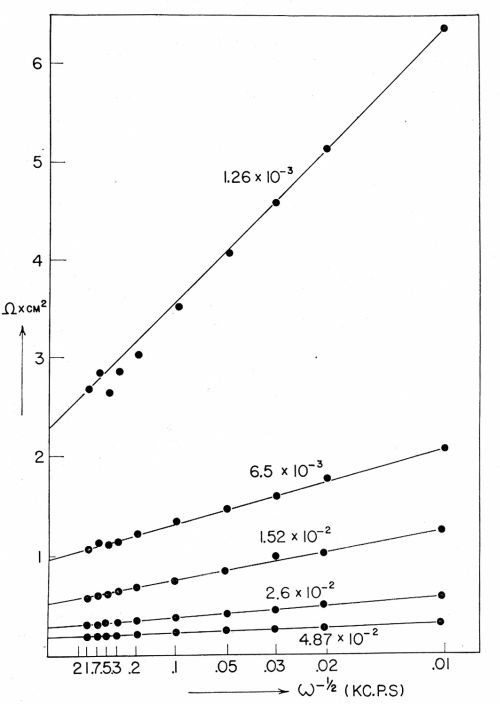
Figure 7 - R_Faradiac as a function of ω^-½.

The value of the transfer coefficient (See Appendix for this and other definitions.) is about 0.4 in the purified solutions of copper sulfate (but about 0.7 to 0.8 in unpurified solutions).  The exchange current density, i_o, in ordinarily purified solutions was about one half to one tenth that in pre-electrolytically purified solution.  A plot of the Faradaic resistance and capacitance is shown in Fig. 7.  It is also relevant to note that the expression for the gradient in the diffusional resistance vs. ω^-½ plot (ω is 2πf, where f is the frequency of the AC used in the bridge by which measurements of the diffusional resistance are made) is

                                          (2)

where a_Cu++ is the activity of the cupric ions (g ions/mL), z is the valency of Cu, F the Faraday constant, A' the area of the electrode to and from which the ions diffuse and D is the diffusion coefficient [thus A' can be obtained from (2)].

Finally, it can be shown that the resistance of the reaction is given by

                                                                            (3)

and that, when ω^-½ = 0,

            R_Reac. = R_Faradaic                                                                   (4)

so that a plot of the Faradaic resistance against ω^-½ gives the reaction resistance when ω^-½ = 0.

Results obtained with equations (2) and (4) are shown in Tables 2 and 3.

Table 2 - Typical theoretical and experimental values of R_Diff.

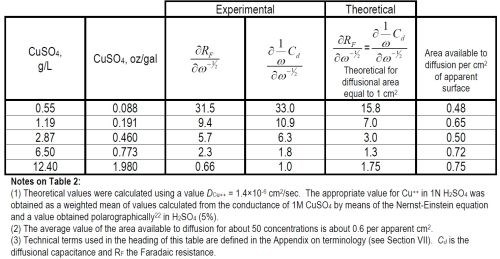
Table 3 - Mean exchange current densities of the forward reaction, Cu⁺⁺_aq. + 2e^-_o ↔ Cu_metal.

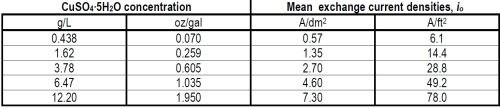
(ii) General interpretive discussion.  As has been shown above, the AC measurements allow us to obtain values of the exchange current density in the case of a copper electrode dipped into an aqueous solution of CuSO₄.  If we do this at various concentrations of copper ions, the exchange current density can be obtained as a function of concentration.  Moreover, it can also be shown that

                                                                              (5)

so that by determining i_o as a function of concentration, the transfer coefficient, α, can be obtained.

Now if the theory of how α should depend upon mechanism is considered, it is possible to make some estimates of value which are characteristic of various rate-determining steps.¹³  These values of α are indeed estimates rather than accurate values for they contain within them the assumption that the energy barrier near to the electrode is a symmetrical one.  The theoretical estimates of α for a divalent ion like Cu⁺⁺ as a function of the rate-determining step are: (i) for transfer from solution to electrode, about one; (ii) for diffusion across the surface, about two; (iii) for nucleation at growth points on the surface, about four.

Now our value of α was found to be about 0.5 for Cu deposition from aqueous CuSO₄ solution, and the nearest of these approximate theoretical estimates to which the experimental value approaches is the first one, namely, that for the ionic transfer reaction from a position in the hydration sheath in the solution to some part of the electrode surface.  Note that the theoretical estimates given for α above, as a function of mechanism, have an appreciable spread in them, probably about ± 50%, because of uncertainty (except with the aid of a rather complex theoretical argument) as to the symmetry of the energy barrier at the surface.  The value of α observed in this case is about half the mean probable value expected to be characteristic of the transfer step, but it is several hundred per cent (quite outside the probable error) less than the values expected for the other possible rate-determining steps mentioned.

The first, and most important, conclusion, therefore, concerns the rate-determining step as being one of "ionic transfer."  Some years ago, this step would have been termed "discharge," or even "neutralization."  However, the metal itself consists largely of ions, bound together by a cement of electrons, and consequently there is little meaning in talking about the "neutralization" of a hydrated ion during metal deposition.  What the term "ionic transfer" means is this: it means the movement of an ion from the position which it reaches in solution just prior to undergoing transfer over the energy barrier, to the position which the still partially hydrated ion reaches when it comes closer to the metal and starts to experience some form of bonding with the metal.  The ion has "transferred" from the solution to the metal surface, and will thereafter undergo several steps in the process of crystal formation until it has built into the surface of the metal, i.e., become a part of the metal lattice, or finally complete the electrodeposition reaction.

Thus, the main interpretive conclusion from this example of fundamental work in metal deposition is that, in the Cu-CuSO₄ (aqueous) system, "ionic transfer" (see above) is the rate-determining reaction.  The characteristics of the kinetics of the electrodeposition of copper should, therefore, follow any influence which may affect the ionic transfer reaction.

It may be asked: How generally valid is this conclusion for the electrodeposition of Cu⁺⁺ ions?  The answer is, of course, that the conclusions apply strictly to the conditions of pH, temperature, concentration, current density and solution composition, etc., in the highly idealized system used.  There is no reason to expect, however, that so long as the Cu⁺⁺ is not highly complexed by addition agents, and so long as the electrode surface is not made very different from that used here, there will be a change in the rate-determining step.  The philosophy of fundamental work, and the very early stage in which fundamental work has been allowed to remain until now, must again be stressed.  It is the foundation results, such as those described here, upon which fundamental research can be built to the point where it may lead to advances in practical plating.

(iii) Implication for metal surface structure.  The results of Table 2 show that diffusion of the Cu⁺⁺ ions up to the electrode surface occurs only to about half of the apparent area - to about one-fifth or one-sixth of the real area.

This behavior suggests a model in which active centers exist on the electrode surface.  The rate-determining ionic transfer from solution to metal thus appears to occur preferentially at these centers, hence denuding surrounding elements of the solution of ions.  A concentration gradient from regions of solution adjacent to inactive parts of the electrode to active parts occurs and the effective area for diffusion is considerably less than the real surface area.  The area on to which ionic transfer can occur must be equal to or less than the area available to diffusion, so that the exchange current per true cm² must be at least five times larger than that given in Table 3 for various concentrations.  The conclusions arising from this discussion are not inconsistent with the formation of smooth deposits experimentally because the deductions here apply only to the mechanism of the rate-determining ionic transfer reaction and its "transfer area."  Growth of planes across the crystal surfaces could still occur as a rapid process all over the electrode surface.

(2) Some purely theoretical concepts and their application to the investigation of the rate-determining step in metal deposition.

It has been mentioned that electrode reactions frequently consist of a number of consecutive reactions.  The theory of the rate-determining step in consecutive reactions has been treated in a quite general way by Laidler, Glasstone and Eyring.¹²  These authors have shown that if a "representative point" in a reaction is considered, and the potential energy of this representative point plotted as a function of distance, the curve will pass through a number of peaks and valleys as shown in Fig. 8.  If one of these peaks is a few kilocalories higher than the others, then the configuration of ions, atoms and/or molecules, the energy of which is represented by this highest peak, is the configuration relevant to the rate-determining step^33,34  All the other smaller peaks then cease to matter for an approximate calculation of the velocity of the overall reaction.

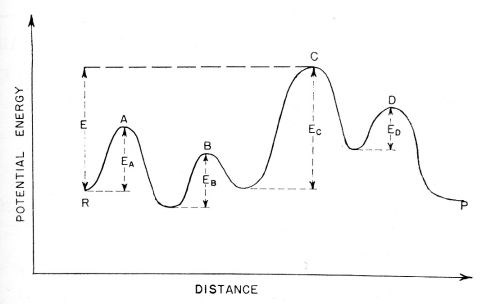
Figure 8 - Activation energies for consecutive reactions: A ⇒ B ⇒ C ⇒ D.  The barrier for process C is the highest and control the rate of the overall reaction in either the forward or backward direction.

This qualitative and general concept has been applied specifically to electrode reactions by Parsons and by Bockris.¹⁴ 

The relevance for metal deposition is this.  If the potential energy of a representative point in a metal deposition reaction can be approximately evaluated as a function of distance from the electrode, it is possible to obtain some purely theoretical indication of the way in which a metal deposition reaction must take place, from the point of view of both path and rate-determining steps.

This purely theoretical approach has recently been made by Conway and Bockris.³⁵  The main difficulties in the calculations arise from uncertainty of the value of the binding energy of the ion to the surface after it has transferred from the solution to the electrode.  Such an approach can be semiquantitative but with a considerable margin of error in the quantities calculated.  Nevertheless,  if the differences between the energies of various steps is sufficiently great, such calculations give diagnostic information concerning the path and rate-determining step, i.e., mechanism of the reaction. 

The results which these calculations indicate are:

(i) It is likely that the path of deposition for the ions concerned is as follows:

(a) Initially there is transfer of an ion from the solution to one of the sites upon the metal shown in Fig. 9, somewhat in the sense discussed above.  During this transfer, the ion remains partly hydrated.  The calculations have shown that the initial transfer step occurs mainly to plane surface sites as shown in the upper diagram of Fig. 9.

(b) Diffusion of the partly hydrated transferred ion occurs across the surface.  It continues until the ions meet a growing edge where further dehydration occurs.  Thereafter, transfer (or diffusion) of an ion may occur until it meets a corner in the growing planes, whereupon further dehydration takes place.  These steps in the deposition of a metal ion are illustrated in Fig. 10.  Such diffusion-dehydration steps continue, the ion being coordinated progressively more with other ions, and less with water, until it is finally coordinated entirely with ions (and electrons), i.e., is part of the metal.  The successive steps leading to the incorporation of a typical ion I into the metal lattice by electrolytic metal deposition, are shown diagrammatically in Fig. 11.  The ion I first arrives at the surface and migrates to a growing edge.  Further adions, A,B,C; K,L,M, and X,Y,Z then arrive as its neighbors, gradually building the adion I into the lattice.  A similar process could also occur at the corner site shown in Figs. 9 and 10.

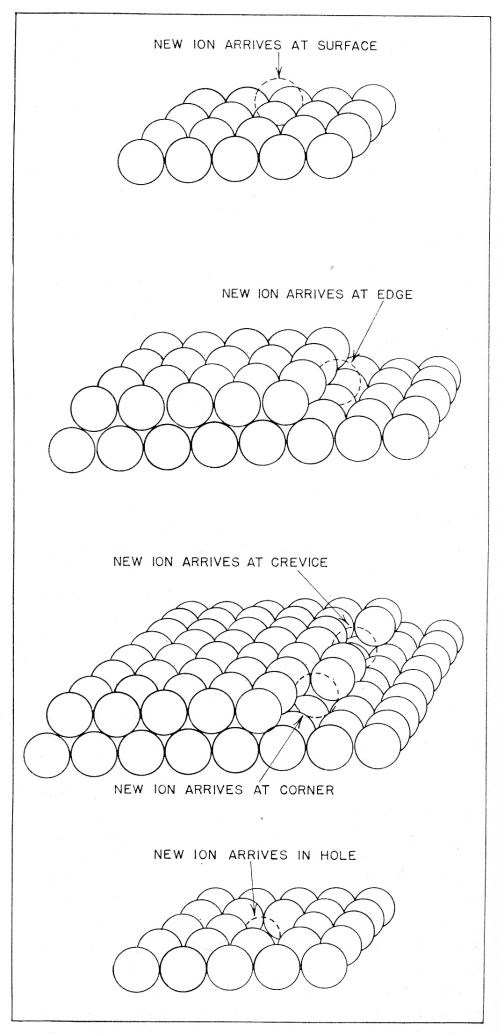
Figure 9 - Sites upon the metal surface to which ionic transfer may occur.  Transfer of ions occurs mainly to the plane surface sites shown in the uppermost diagram.

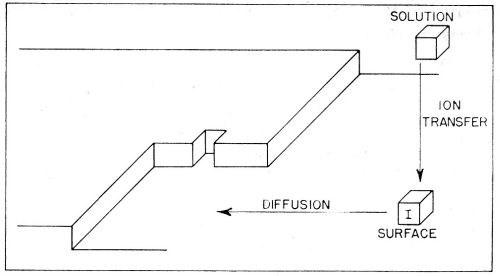
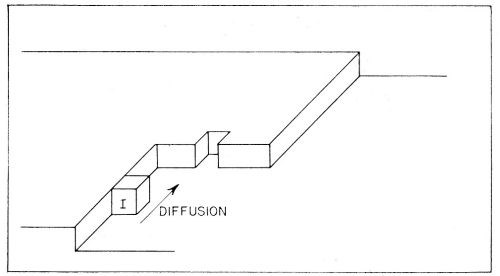
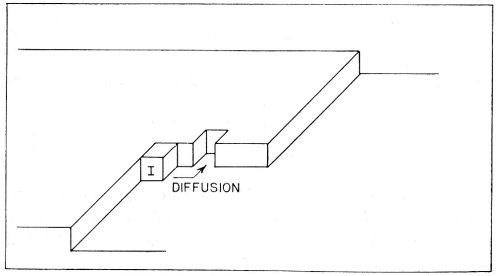
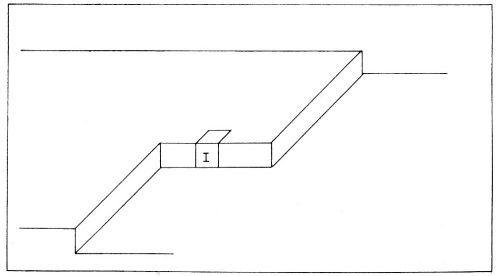
Figure 10 - Consecutive ionic transfer, surface-diffusion and edge-diffusion of adsorbed ions during the building of the metal lattice in electrolytic metal deposition.

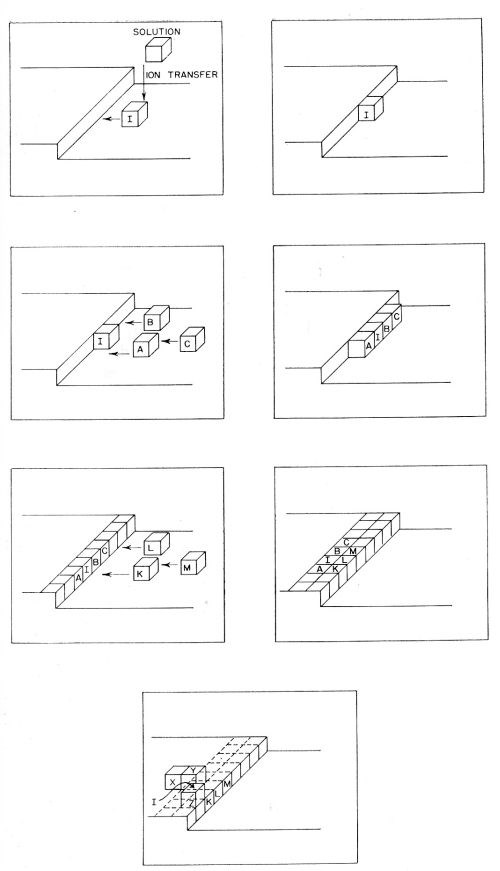
Figure 11 - Incorporation of a typical metal atom or ion I into the lattice by consecutive transfer and diffusion of I together with participation of other atoms A,B,C; K,L,M and X,Y,Z arriving as its neighbors in the growing lattice.

(ii) Along this path, the potential energy-distance plots show at high current density one pronounced maximum, namely, that for the transition (or transfer) from the solution to the electrode.  The potential energy of the maximum of the energy barrier here is greater than any other potential energy in the system and thus in the cases for which this result has been obtained, the rate-determining step is probably the ionic transfer reaction at the solution-metal interface.

This conclusion of the importance of an electron or an ion transfer step in determining the rate of deposition from solutions in the absence of complexes, does not necessarily apply at low current densities where the number of growth points on the surface is relatively small.  Here the diffusion of adions may influence the rate-controlling step because the relative absence of growth positions tends to decrease the rate of diffusion between the site of transfer and the point where lattice building occurs.

V. Relevance of the fundamental work discussed here to electroplating

The general relation between fundamental work on electrodeposition and industrial work has already been mentioned (in IV, 1) and the relevance of the introductory work which is discussed here is that it is one of the initial pieces of work which begins a build-up of fundamental knowledge.  When the fundamental work has caught up with the more empirical practical work, the future potentialities of the industry for development are very great indeed, because the necessary insight will be available to shorten work on the solution of new problems.

Even at this very early stage, certain relevant direct connections to mechanisms of practical plating can be seen.  The long known facts of the effects of additives in solutions from which metal deposition is occurring, can now begin to be expressed in terms of a model picture.  The transfer of the ion from an hydrated state to a state on the electrode surface indicates that modification of the energy of the ion in solution, e.g., by complex formation or change of solvent, will lead to modification of the rate and possibly the mechanism of the transfer process.  The reason that adsorbed additives have a marked effect on the course of the reaction is that they modify the sites available to which transfer can occur, and also slow down the surface diffusion of transferred ions and hence affect the lattice growth.  The concept of the existence of peaks is consistent with results on micro-throwing and its dependence on the presence of additives.³⁴  Polar additives will tend to be preferentially adsorbed at regions of high field strength - at peaks - and hence may inhibit further transfer of ions at the peak, thus tending to produce more uniform deposits.  pH effects can be understood as influencing, among other things, the relative rate of hydrogen deposition compared with that of the metal.  Significant hydrogen deposition will cause the presence of adsorbed hydrogen on the electrode which in turn will modify surface diffusion of metal ions and crystal growth particularly on those metals, e.g., nickel, having a large affinity for hydrogen atoms.

VI. Summary

1. This paper constitutes an attempt to explain the type of work being done in fundamental research on the molecular mechanism of metal deposition.

2. The general subjects of investigation relevant to finding out the atomic-ionic mechanism of electroplating are: (a) the structure of the electric double-layer at the (solid) metal-solution interface, (b) the constitution of the ions in solutions, which are the source of the electrodeposited metal and (c) the path and rate-determining step in the actual metal deposition reaction.

3. The technique of fundamental work attempts to reduce any system examined to one with the least possible number of uncontrolled variables.  This technique is thus usually somewhat complex.  In particular, special techniques - of which pre-electrolysis is an excellent example - must be used for purification of solutions and electrodes must be introduced into the solution in a manner such that their surfaces remain free from contamination.

4. A brief outline is given of the experimental technique used in one piece of fundamental work.

5. "The kernel of the objective in fundamental work on the electrodeposition of metals is the evaluation of the nature of the rate-determining step."  This statement is discussed.

6. Some experimental results in one fundamental investigation are described.

7. The interpretation of these results is discussed.  The experimental data are consistent only with the view that ionic transfer is an important step in the rate of exchange of copper ions between metal and solution.

8. The metal surface, cleaned under the conditions described, appears to have some active sites to which preferential diffusion occurs.

9. A purely theoretical approach to the mechanism of electrodeposition is outlined.  It supports the interpretation of the experimental results in Cu/CuSO₄.  It suggests that the rate-determining step deduced may have a wide relevance.

10. The relevance of this fundamental work to practical progress in industrial electroplating is outlined.

11. An informal explanation of the terminology of fundamental work in electrodeposition is given in an appendix.

Acknowledgements

Many thanks are due to the American Electroplaters’ Society for their encouraging support of this work, and particularly to the members of the Project Directing Committee for stimulating discussion during its course.

VII. Appendix and terminology

The following terms will be briefly defined or discussed.  The explanations given here are brief and informal.  Formal definitions are given in Reference 24.

(i) Reversible (or equilibrium) potential.  This is, e.g., the potential which a metal electrode exhibits when it is in contact with metal ions of the same species in the absence of net current flow.

(ii) Polarization.  This is a general term which means roughly "changes in potential which occur as a result of the passage of a current across the electrode-solution interface."  Consequently, electrodes which exhibit changes of potential upon passage of current are said to be "polarized."  The term "overpotential" (see below) is often used synonymously with "polarization" although the former term can be defined more rigorously.

(iii) Overpotential (η).  This is the potential of an electrode which is passing current measured with reference to the potential of the electrode in the same solution when it was not passing current.

There are several kinds of overpotential.  In all except the German literature, they are divided into three types: one in which the reaction is controlled by ohmic (or resistive) factors in films on the electrode (e.g., the oxidation of tantalum); one in which diffusion in solution limits the supply of reacting entities to the electrode, (such as Cl₂ at an electrode) and one in which activation of reactants at the electrode-solution interface is necessary for the reaction to proceed at a rate corresponding to the current density (for example, in the hydrogen or oxygen evolution reaction).

(iv) Transfer coefficient.  When DC polarization of an electrode occurs and under certain simplifying conditions,

                                                                                           (6)

where a is the Tafel constant characteristic of the electrode process, or alternatively

                                                                                                (7)

is the experimental result found for the relation between over-potential, η, and current density, i.  In this equation, a, which is constant with current density and (usually)²⁵ with temperature, is called the transfer coefficient, and i_o, the exchange current (see below).  The name is not altogether a logical one, but some sense in it may be seen if Eq. (7) is written as:‡

            i = i_oe^-aηF/RT                                                                                                                 (8)

Thus, α is the fraction of the energy ηF due to the overpotential and since the current is exponentially dependent upon ηF, α is the coefficient which determines the rate at which ions are, e.g., transferred from the solution to the electrode.

(v) Exchange current density.  Consider a copper electrode dipped in copper sulfate and weakly polarized cathodically.  Like any chemical reaction, an electrode reaction has a backward and a forward direction, so that, in the passage of a net cathodic current (the net current is the current which is measured by the ammeter) the current associated with deposition must be greater than that associated with dissolution.  In general, the observed net current (i_c) can be expressed as

                                                                                             (9)

where the  is the current density associated with the "forward" (or cathodic deposition) part of the reaction and  is that associated with the reverse (or anodic dissolution part.

Now, when the electrode is no longer polarized, it can have no further net current flowing across it, i.e., i_c = 0.  Hence from (9),

                                                                                                      (10)

i.e., the partial cathodic and anodic current densities are equal in magnitude and opposite in direction.  These equal and opposite current densities at the reversible potential are called the ''exchange current density," and represented by i_o (Eqs. 7 and 8) which is usually quoted in amp/cm² independent of direction.  Frequently, it is loosely called "the exchange current."

The exchange current density is a central concept in electrode kinetics.  Thus, the current density which is attained by a certain electrode reaction for a given amount of polarization (i.e., for a given overpotential), is simply proportional to the exchange current density.  Hence, the exchange current density is a direct measure of how fast or slowly a reaction occurs at a given overpotential.  Reactions like the evolution of hydrogen on mercury, which has a small value for its exchange current density, namely, about 10^-13 A/cm² (10^-10 A/ft²) are called "slow" reactions, and electrode-solution interfaces at which such reactions occur are said to be very "polarizable."  Reactions such as the deposition of Ag⁺ ions from an aqueous AgNO₃ solution have an exchange current density of about 10^-4 A/cm² (10^-1 A/ft²) and are said to be fairly fast.  Reactions such as the deposition of Na⁺ onto Hg have i_o values of about 10^-2 A/cm² (10 A/ft²) and are regarded as very fast reactions,²⁷ (sometimes they are also called "reversible reactions").

The term "exchange current" seems to have been introduced by Bowden and Agar.²⁹  It is a logical one: i_o is the rate (in terms of current density) at which the ions of a solid metal enter the solution at the reversible potential; and it is also the rate at which ions deposit on the electrode from the solution.  Thus, it is the rate at which ions in metal and solution exchange between the two phases at the reversible potential.

(vi) Rate constant.  In ordinary reaction kinetics, the rate of a simple reaction is taken as equal to the product of the active masses of the reactants, multiplied by a constant called the rate constant.  In electrode kinetics, the current density is the analogue of the rate of the reaction.  Hence, the exchange current density must contain the product of a rate constant and concentration, and it is possible to show²⁸ that the relation between rate constant and exchange current is

                                                                                         (11)

where  is the rate constant for the forward reaction, n_o is the number of electrons which are involved in one of the rate-determining steps, and Π indicates the product of the various activities a₁, a₂, etc., of the reactants 1, 2, etc., taking part in the forward direction of the overall reaction.

(vii) Activation control.  Frequently, and particularly when there is a large supply of the depositable metal ions in the solution, the rate of the electrode reaction is essentially controlled by the actual rate of the electrode process occurring at the interface.  Since ions have to be chemically or electrochemically "activated" in order to undergo these reactions, the control of the rate of the reaction in such cases is logically called "activation control."

(viii) Diffusion control.  If the activation controlled rate of any electrode reaction becomes sufficiently fast, it exhausts the ions in the vicinity of the electrode-solution interface.  Their diffusion to the electrode then becomes the slow step in the reaction, i.e., the rate-determining step.  Such reactions are called "diffusion controlled" reactions.

(ix) Voltaic adsorption³⁰.  This is the kind of adsorption which occurs at a double-layer [see (xi)] when the only forces causing the adsorption are purely electrostatic, (Fig. 12A).

(x) Specific adsorption.  This is the adsorption which occurs when there is an attachment of ions or molecules to the electrode in which the bond (Fig. 12B), is not purely an electrostatic bond.

Figure 12 - A. Voltaic or electrostatic adsorption (i.e., nonspecific); B. Specific adsorption.³⁰

(xi) Double-layer.  When an electrode potential difference exists at an electrode interface, electronic charges accumulate in the metal at its interface and a corresponding charge of ions is attracted from the solution to a region near the interface of the metal.  This system, consisting of opposite charges facing one another at the interface, is called the double-layer.

(xii) Equivalent circuit.  It is often convenient to represent entities which control the relation between current density and potential at an electrode under alternating current in terms of the imaginary equivalents of these entities regarded as resistances and capacitances arranged to form a circuit that would have equivalent electrical properties, e.g., with regard to the behavior of an AC in the circuit (Fig. 6).  This is done in order to facilitate deduction of relations between experimental quantities such as a resistance measured on a bridge, and the exchange current density of an electrode reaction in a cell, the electrode-solution interfaces of which are the source of the resistance.  For example, suppose the double-layer between a mercury electrode and a concentrated KCl solution is considered.  In this case, the actual configuration in the absence of current flow is very nearly that of two layers of charges of opposite sign, separated by a vacuum.  This strongly suggests that in any electrical circuit which contains the Hg/concentrated KCl interface, the correct way to represent the corresponding double-layer is as a condenser of capacity C_L (see below).

Suppose now ions were discharged across the double-layer condenser.  Then, current could be used up at the double-layer in two ways; firstly, by charging of the condenser (regarded as a simple capacitance), and secondly, by actual ionic transport across the double-layer.  The "condenser current" can be dealt with in terms of the simple equations of electric circuit theory for the charging of a condenser, and the "Faradaic current" [that for ionic flow across the double-layer - see (xviii)] may be treated in terms of a resistance, R_L (see below).  The condenser current and the Faradaic current are both simultaneous ways of passing current across the double-layer and, therefore, the "equivalent circuit" for the passage of current across the double layer in the example quoted (simplified by the neglect of consideration of diffusion) is a resistance and capacitance in parallel.

Other processes at electrodes can also be represented in terms of ohmic or capacitative components, and then the usual equations of AC theory may be applied to the whole equivalent circuit.  If, then, it is possible to find an explicit relation between, e.g., a certain resistance in the equivalent circuit, and some property of the electrode reaction, then AC theory applied to the measurements may allow the extraction of the value of that resistance alone, from the impedance of the whole interface, and the explicit relation mentioned would then allow evaluation of the parameter of the electrode reaction.

(xiii) Diffusional resistance.  There is always some difficulty in bringing up ions from the bulk of the liquid to the electrode, even though, at low current densities, this may not be the rate-determining step.  This difficulty in diffusion can be expressed as a resistance (and an explicit expression can be deduced relating this resistance to the diffusion coefficient and concentration of the diffusing entity, etc.).

(xiv) Diffusional capacitance.  Consideration of the properties of AC in the vicinity of an electrode, the potential of which is controlled only by the concentration of ions with which the metal is in contact, shows that the properties of the current-potential relation are those which would arise were the diffusion of ions to and from the electrode surface to be regarded as acting as a capacitance and a resistance, the former therefore, being called the "diffusional capacitance."  This capacitance is a pseudo-capacitance in the sense that it represents certain physical phenomena, which act as though they constituted a capacitance, although they do not in fact appear to constitute a capacitance in the normal sense.

(xv) Double-layer capacitance.  This has been described above (under xii).

(xvi) Reaction resistance.  The electrode reaction itself (apart from the diffusion which precedes it) represents a resistance (i.e., the difficulty of overcoming the energy barrier at the electrode) and this is the most important term in the AC behavior of an electrode, because it is the term by which the AC behavior is connected with the metal deposition phenomenon.

(xvii) Double-layer resistance.  If the double-layer itself acts not only as a pure capacitance but rather as a leaky capacitance, like a "lousy" condenser, then it may be said to have a double-layer resistance.

(xviii) Faradaic impedance.  The term "Faradaic" (cf. xii) is used to describe those aspects of processes at electrodes which involve current flow in accordance with Faraday's laws, as distinct, e.g., from current used not in producing deposited metal in accordance with Faraday's laws, but in charging the double-layer.  Thus, a combination, for example, of the reaction resistance together with the diffusional resistance and the diffusional capacitance, represents the Faradaic impedance of the electrode reaction.

(xix) Double-layer impedance.  The double-layer impedance arises from the double-layer resistance, R_L and the double-layer capacitance, C_L as represented in Fig. 6.  The whole electrode impedance is made up of the Faradaic impedance and the double-layer impedance.

References

1.   D.C. Grahame, Chem. Rev., 41 (3), 441 (1947).

2.   B.E. Conway, J.O’M. Bockris & B. Lovrecek, Comite inter, thermodynam. et. cinet. electrochim. Comt. rend, reunion, VI, 207 (1954).

3.   R. Parsons, Modern Aspects of Electrochemistry, Ch. III; J.O’M. Bockris, Ed., Academic Press, New York, NY, 1955.

4.   M.T. Simnad, Proc. Symposium, Institute of Metals, p. 23 (1952).

5.   J.O’M. Bockris & P. Jones, Nature, 171 (4360), 930 (1953).

6.   J.O’M. Bockris & B.E. Conway, J. Chem. Phys., 28 (4), 707, (1958).

7.   J.O’M. Conway, R.G. Barradas & T. Zawidzki, J. Phys. Chem., 62 (6), 676 (1958).

8.   J.O’M. Bockris, Quart. Rev., III, (2), 173 (1949).

9.   B.E. Conway & J.O’M. Bockris, Modern Aspects of Electrochemistry, Ch. II, Academic Press, New York, NY, 1955.

10.  J.O’M. Bockris, L. Young, G.J. Hills & I.A. Menzies; J.O’M. Bockris, G.J. Hills, L. Young and D. Inman; in course of publication [as of 1959].

11.  T.G. Pearson & J. Waddington, Discussions Faraday Soc., 1, 307 (1947).

12.  S. Glasstone, K.J. Laidler & H. Eyring, Theory of Rate Processes, McGraw-Hill, New York, NY, 1941; p. 99.

13.  J.O’M. Bockris, Modern Aspects of Electrochemistry, Ch. IV, Academic Press, New York, NY, 1955.

14.  W. Lorenz, Z. Elektrochem., 57, 381 (1953); R. Parsons & J.O’M. Bockris, Trans. Faraday Soc., 47, 914 (1951); B.E. Conway & J.O’M. Bockris, J. Chem. Phys., 28 (4), 707 (1958).

15.  J.O’M. Bockris & B.E. Conway, Trans. Faraday Soc., 45, 989 (1949).

16.  C. Wagner, J. Electrochem. Soc., 101 (4), 181 (1954).

17.  A.N. Frumkin & G.M. Florianovich, Doklady Akad. Nauk. U.S.S.R., 80, 907 (1951).

18.  J.O’M. Bockris, J. Electrochem. Soc., 98, 153 (1951).

19.  J.O’M. Bockris, B.E. Conway & W. Mehl, J. Sci. Inst, 33 (10), 400 (1956).

20.  A.M. Azzam, J.O’M. Bockris, B.E. Conway & H. Rosenberg, Trans. Faraday Soc., 46, 918 (1950).

21.  G.N. Lewis & R.F. Jackson, Z. Physikal. Chem., 56, 1207 (1906).

22.  H. Gerischer, Z. Elektrochem., 54, 366 (1950).

23.  N.K. Adam, Physics and Chemistry of Surfaces, Clarendon Press, Oxford, UK, 1938; p. 174.

24.  J.O’M. Bockris, et al., Comite intern, thermodynam. et cinet. electrochim. Compt. rend, reunion, 111, 444 (1951).

25.  J.O’M. Bockris, R. Parsons & H. Rosenberg, Trans. Faraday Soc., 47, 766 (1951).

26.  J.O’M. Bockris, W. Mehl, B.E. Conway & L. Young, J. Chem. Phys., 25 (4), 776 (1956).

27.  J.E.B. Randles and K.W. Somerton, Trans. Faraday Soc., 48, 951 (1952).

28.  J.O’M. Bockris, Modern Aspects of Electrochemistry, Ch. IV, Academic Press, New York, NY, 1955; p. 196.

29.  F.P. Bowden & J.N. Agar, Ann. Rep. Chem. Soc., London, 35, 90 (1938).

30.  S.R. Craxford, Trans. Faraday Soc., 35, 85 (1940).

31.  C. Wagner, J. Electrochem. Soc., 97 (3), 71 (1950).

32.  J.O’M. Bockris, Modern Aspects of Electrochemistry, Ch. IV, Academic Press, New York, NY, 1955; p. 219.

33.  R. Parsons, Trans. Faraday Soc., 47, 1332 (1951).

34.  J.O’M. Bockris, Modern Aspects of Electrochemistry, Ch. IV, Academic Press, New York, NY, 1955; p. 180.

35.  B.E. Conway & J.O’M. Bockris, Proc. Roy. Soc. A (London), 248 (1254), 394 (1958).

36.  J.L Hoard & H.H. Nordsieck, J. Am. Chem. Soc., 61 (10), 2853 (1939).

Extended author bios

Brian E. Conway (1927-2005), once referred to as “the Dean of Electrochemistry in Canada,” was born in London, England.  He commenced undergraduate studies in 1944 at the Imperial College of Science and Technology, University of London, where he held a five-year scholarship.  In 1946 he was awarded the degree of B.S.C. (Honors) and Ph.D. (1949) and the Diploma of Imperial College.  From 1949 until 1954 he worked at the Chester Beatty Research Institute of the University of London as research lecturer in the Department of Professor J.A.V. Butler, where he carried out research on the theory of electrode processes and the physical chemistry of polymeric electrolytes.  In 1956 he came to the University of Pennsylvania as a special Research Fellow and was subsequently appointed Assistant Professor, carrying out theoretical work mainly on the application of the absolute reaction rate theory of chemical reactions to electrochemical processes including proton transport, proton discharge and metal deposition.  In 1956 he was appointed to the permanent staff of the University of Ottawa, Ottawa, Canada, as Associate Professor.  His career at the University of Ottawa turned out to span five decades.  He was promoted to the rank of Full Professor in 1962.  He served as Department Chairman from 1966-1969 and 1975-1980.  He was a Killam Senior Research Fellow from 1983-1985 and the Natural Sciences and Engineering Research Council (NSERC) - Alcan Professor of Electrochemistry from 1987-1992.  He then retired, with the title of Professor Emeritus.  He passed away at the age of 78, in 2005.

At the time of the publication of this paper, Dr. Conway had authored two books, Electrochemical Data and Electrochemische Tabellen," and he went on to author two more.  In 1959, he had published 61 research papers in scientific journals, which expanded over the years to more than 400.  He was a member of the Editorial Board of the then new Journal of Electroanalytical Chemistry.  Among the many honors and awards were Fellow of the Royal Society of Canada (1968), the Chemical Institute of Canada Medal (1975), the American Chemical Society Kendall Award in Surface Chemistry (1984), the Electrochemical Society Henry Linford Medal (1984), the Olin Palladium Medal and Award of the Electrochemical Society (1989), the Galvani Medal of the Italian Chemical Society (1991) and Fellow of the Electrochemical Society of America (1995).

Dr. Conway’s research contributed much to the understanding of electrode kinetics, particularly those of hydrogen evolution and the very earliest stages of metal oxidation.  His work in applied electrochemistry has allowed the development of rechargeable, compact batteries and supercapacitors for cellular phones, laptop computers and communications systems.

John O'Mara Bockris (1923-2013) was born in Johannesburg, South Africa, and educated in London, England.  He studied modern languages, physics and chemistry at the University of London.  He obtained his Ph.D. in 1945, joining the faculty of the Imperial College of Science of the University of London in that year.  In 1952 he was awarded the degree of D.Sc. by the University of London for "authoritative contributions to the field of electrochemistry."  In 1954 he was appointed Professor of Chemistry at the University of Pennsylvania.  In 1972 he became Chair of the Department of Physical Chemistry at the Flinders University in Adelaide, South Australia.  He returned to the United States in 1978 with an appointment as Distinguished Professor of Chemistry at Texas A&M University.

Dr. Bockris, perhaps “the Dean of Electrochemistry in the United States,” has over 700 publications to his credit, including two dozen books.  Among those books, are the primary text, Modern Electrochemistry and the 33-volume (to date) series, Modern Aspects of Electrochemistry.  In addition, he published the ten-volume Comprehensive Treatise in Electrochemistry.  He was a founding member of the International Society of Electrochemistry (ISE) in 1949 (then called CITCE).  Among the multitude of honors that he has received are the Faraday Medal of the Chemical Society of Great Britain (1979), the American Chemical Society (ACS) Award in Contemporary Technology (1988), an Honorary Degree in Law at Hokkaido University (Japan) (1991) and the Linford Medal of the Electrochemical Society (ECS) for “Excellence in Teaching” (1995).  He passed away at the age of 90 in 2013, in Gainesville, Florida.

Dr. Bockris’ research dealt mainly with the mechanism of electrode processes and the constitution of molten salts and silicates.  He also carried out a number of investigations in other fields, namely on the deviations from ideality of systems containing carbon in iron, on the solubility of oxygen in iron and of non-electrolytes in solutions of electrolytes, the adsorption of gases in metals and on magneto-chemistry.  Dr. Bockris worked in virtually every area of electrochemistry, producing dozens of Graduate students who are experts in their own right.  He retired from Texas A&M in 1990.