Published 1/12/2017

The Plater and Pollution - The 18th William Blum Lecture

This article is a re-publication of the 18th William Blum Lecture, by Dr. Joseph B. Kushner, presented at the 64th AES Annual Convention in Los Angeles, California, on June 27, 1977.

Edited by: PF Editorial Team

Editor’s Note: Originally published as Plating & Surface Finishing, 64 (8), 24-26, 28, 30 (1977), this article is a re-publication of the 18^th William Blum Lecture, presented at the 64th AES Annual Convention in Los Angeles, California, on June 27, 1977. Only excerpts from the lecture were published, but the material available did cover the major portions of his talk. A printable PDF version is available by clicking HERE.

The First Job - How Dr. Kushner became interested in plating rinse waters

Besides being a renowned expert in the field of electroplating, Dr. Joseph B. Kushner was also a colorful personality who had a flair for telling interesting stories. Before he launched into the technical discussion as the year's William Blum lecturer, he delighted the audience with his account of how he became involved in the electroplating business and why he became interested in plating rinse waters.

Dr. Kushner's first break into electroplating came in 1934 when he was a fresh chemical engineering graduate of the Cooper Union Institute of Technology. He went to work for a costume jewelry house that he recalls as being typical of those days.

"Unfortunately, that shop was also typical of some of the shops you see today!" exclaims Dr. Kushner. "Soaking wet floors, slippery wooden duckboards, steaming, unventilated tanks of plating solutions, acid dips and cyanide, the kind of lighting you could go blind with. The place was loaded with wall-to-wall OSHA violations!" He had high hopes, however, that they'd soon recognize his talents and set him up with a chemical laboratory.

His hopes were quickly doused, as the "trusted employee" who was assigned to teach him a great deal was more interested in guarding his own position. He confined young Kushner to dipping, rinsing and shaking while he made up the gold solutions behind closed doors.

After about three months, the president of the company put young Kushner on a special investigative assignment: to find out why the company was using more gold than it should. That's where Dr. Kushner's interest in plating rinse waters actually began. He carefully studied the entire plating operation and singled out the dragout crock as the culprit.

"Everything that was gold plated was first dipped into that crock," says Dr. Kushner, "and I noticed that the color of the solution in the crock was just about that of the gold plating solution itself. Since I had never seen that water changed in the few months I was there, I realized the gold plating bath was going down the sewer via the dragout tank. For me, it was like Columbus discovering America."

His attempts to do a thorough dragout study were thwarted by the "trusted employee" who ran immediately to the president and complained Kushner was holding up production.

When the president questioned Kushner about his findings, Kushner replied, "Well, I haven't made any calculations yet, but I would say theoretically you could be losing as much as maybe 50 ounces of gold a year."

The president didn't relish this revelation. "Fifty ounces! We're losing more than ten times that! Kushner, you're fired!"

Although Kushner's ideals had been trampled on, he soon met a gold refiner and convinced him that there was a gold mine in prepared gold plating solutions and salts for commercial applications. He was signed on for a glorious salary of $35 per week and he waived all patent rights to develop and produce salts and solutions.

"My first result was 'Robinson's Assayed Gold Plating Solution,' which was the forerunner, as old-timers will recall, of all the commercial gold plating solutions. I made the discoveries and developments and Robinson made the money," Dr. Kushner sighs.

Occasionally, virtue does get its own reward, however, Dr. Kushner learned through the grapevine why his former employer used so much gold; the "trusted employee," when mixing up the gold solutions behind closed doors, each time cut off some gold for himself. When it was discovered that most of the missing gold didn't go down the drain but instead went in the pocket of the "trusted employee," he became a former employee, too.

With that preamble, Dr. Kushner's lecture follows.

Slowly but surely we are beginning to learn that, besides air, water is our most precious natural resource and that it must be conserved in the same way that we conserve gold or silver. Contrary to common belief, the supply of usable water is not endless. . . .

What would happen if there were no water? It would result in a tremendous social upheaval too dreadful to even contemplate. Worse than an earthquake, worse than a revolution.... Water is not something you can take for granted; it is more precious than diamonds or rubies - you can do without them - but you can't do without good water for living and for plating. My philosophy has always been on the side of saving water and chemicals wherever, whenever it is possible to do so. . . .

Study of dragout

The subject of dragout intrigued me and I made a study of it. In the January 1935 issue of Metal Industry (later Metal Finishing),¹ I published my first paper, "Losses from Recovery Rinse Tanks." It was the first quantification of the dragout process and it clearly demonstrated that when a stagnant rinse tank is used for recovery of gold plating salts, the concentration of solution in the recovery tank will gradually become equal to that in the plating bath (Fig. 1).

Figure 1 - Build-up of plating salts in a dragout tank.

The derivation assumed that there was instantaneous mixing in the stagnant tank, which is a source of error. A much later development of mine shows that this error is not too serious and that it can be allowed for. The formula derived was:

$C=C_{o}\left [1-\left ( 1+\theta /V \right )^{-n} \right ]$ (1)

where C is the concentration in the dragout tank after n rinsing cycles or its time equivalent, t, C_o is the concentration in the plating bath, θ is the average dragout per rinsing cycle, and V is the volume of the dragout tank, all in consistent units. An alternative form of the formula is:

$C=C_{o}\left [ 1-exp\left ( -\theta n/V \right ) \right ]$ (2)

where exp(-θn/V) refers to e, the base of Napierian logarithms, raised to the -θn/V power.

The problem of dragout, which years ago was insignificant except in the case of precious metal plating, has turned out to have tremendous significance today because it is the major source of pollution produced by the plating industry. As illustrated in Fig. 2, the droplets of plating solution that hitchhike along with the plated work wind up in the sewers and waterways. When platers relied on dilution to cure everything, there was little or no interest in dragout. Now, with authorities talking about parts per billion or even undetectable concentrations in plating plant effluents, and with water prices on the rise, the picture has changed drastically.

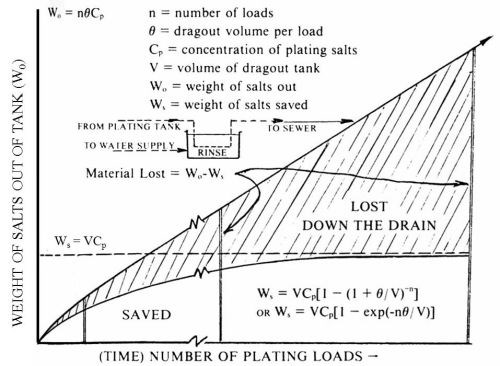
Figure 2 - Dragout - the trouble maker!

In the following years, I became even more interested in the subject of water in the plating room, and in 1942 the Monthly Bulletin of the AES published my paper on "Impurity Build-Up in Plating Tanks."² This showed how impurities in the water supply build up in plating baths and how impurities which enter the bath from impure anodes, chemical or electrochemical decomposition become more concentrated with time in warm plating baths. Everything depends on the ratio of the water evaporation rate of the bath to the dragout rate. The formulas derived were quite simple. For impurities in the water supply:

$C=C_{w}\left ( 1+E/\theta \right )$ (3)

where C is the limiting concentration of the impurity in grams per liter, C_w is the average concentration of the impurity in the plating water supply, E is the plating bath evaporation rate in liters per unit time and θ is the dragout rate in liters per unit time. For impurities forming in the plating tank, the formula is:

$C_{i}=I/\theta$ (4)

where C_i is the limiting concentration of the impurity in the plating bath in grams per liter, I is the number of grams of impurity forming in the bath per unit time and θ as before is the dragout rate in liters per unit time. . . .

As can be seen in Fig. 3, in the case of impurities, the dragout is a purifying factor. Without it, as long as there is plating bath evaporation, the impurity concentration will build up indefinitely in each case. With dragout, the impurity concentration reaches a limiting value. With the time factor included, the formula for a water borne impurity reads:

$C=C_{w}\left ( 1+E/\theta \right )\left [ 1-exp\left ( -\theta t/V \right ) \right ]$ (5)

where C is now the concentration at any time, t, and all the other symbols have the meaning given to them previously; V is the volume of the plating tank in consistent units. For bath generated impurities, the formula reads:

$C_{i}=\left ( I/\theta \right )\left [ 1-exp\left ( -\theta t/V \right ) \right ]$ (6)

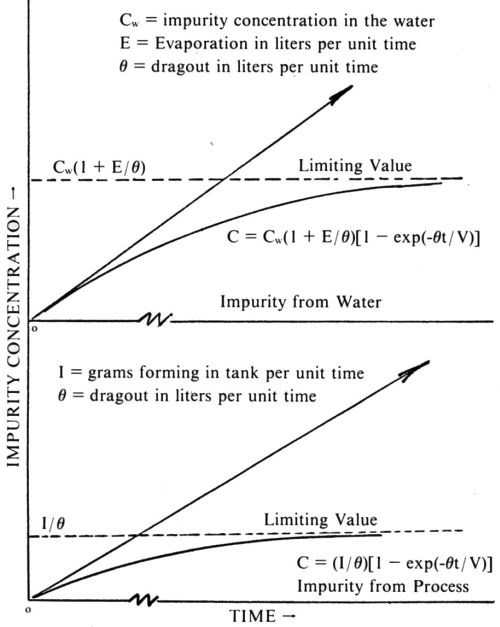
Figure 3 - Impurity build-ups.

Once again what was considered to be a very minor item in the day-to-day operation of a plating shop became one of major importance because, on the face of it, if one doesn't want any chemicals going down the drain, then the easiest thing to do is to feed them back to the plating tank through a series of slowly flowing dragout tanks (rinse tanks). But in so doing, the impurities are concentrated and may indeed reach intolerable levels. In the early fifties I presented formulas which enabled one to calculate the limiting concentrations which impurities could reach when a series of very slowly flowing dragout tanks (rinses) return the diluted plating solution back to the bath. If the ratio of the evaporation rate, E, to the dragout rate, θ, is symbolized by A (E/θ = A) and n is the number of dragout tanks used, the formulas are;

$C=C_{w}\left ( A^{n+2}-1 \right )/\left ( A-1 \right )$ for water borne impurities (7)

$C_{i}=\left ( 1/\theta \right )\left ( A^{n+2}-1 \right )/\left ( A-1 \right )$ for tank formed impurities (8)

As I pointed out previously, we are dealing with very small quantities and everything will depend on the value of A. A few examples will make it clear. Consider a 250 g/L chromium plating bath. The water supply carries 10 ppm of chlorides. The dragout rate is 0.1 L/hr (low) and the evaporation rate is 2 L/hr. With no return feed tank, n = 0 and C = 10(20²- l)/(20-1) = 210 ppm. With one return feed C = 10(20³ - 1)/(20 - 1) = 4210 ppm. With two return tanks, C = 10(20⁴ - l)/(20 - 1) = 84210 ppm.

Some engineers who should know better have stated that the buildup of impurities in a plating bath is exaggerated and need not be considered. In the old days, when dragout rates exceeded evaporation rates this was true, but today, when the evaporation rate must exceed the dragout rate for successful recycling, this is no longer true. Take the same example given previously, except that now the dragout rate and the evaporation rate will be reversed. Thus A becomes equal to 0.1/2 = 0.05 and for no feed return tank, C = 10.5. With one return feed, C = 10.53 ppm, and for two recovery tanks, C = 10.53. Indeed for ten recovery tanks, it is still 10.53 ppm. But, as you saw before, with A larger than unity, the impurity build up can reach very high values!

Development of rinsing technology

The next step in the development of the technology of rinsing was the rinsing equation itself. The first quantitative development with the correct approach (rinsing as an intermittent process) was published in Plating³ in 1949. It was based once again on the assumption of perfect mixing. The formula, which has been modified by other authors, gives the equilibrium concentration of plating salts in a rinse tank to be:

$C=\left ( \theta C_{p}/V \right )exp\left ( -qt/\theta \right )/\left [ 1-exp\left ( -qt /V\right ) \right ]$ (9)

where C_p is the concentration of the salt in the plating bath, V is the volume of the rinse tank, q is the rinse water flow rate in liters per unit time, and t is the actual time the item is in the rinse tank. This equation gives the curve shown in Fig. 4. If this is integrated to give the average value over a long time period, the result comes out to be:

$C=C_{p}/\left ( 1+qt/\theta \right )$ (10)

which is exactly the result one obtains by assuming a continuous process and solving the resulting differential equation for the limiting value. When water was no object and there was no EPA, qt could be made as large as desired and the 1 in the parenthesis could be neglected, resulting in a very simple form of the rinsing equation:

$C=C_{p}\theta /qt$ (11)

Figure 4 - Rinsing: old model (perfect rinsing).

This paper raised quite a stir when in it I suggested such blue sky ideas as "long distance" rinsing and the equivalent of "chemical" rinsing to save water. These methods are now facts of life in the plating industry, both here and abroad.

In terms of the rinsing criterion⁴ (the ratio of the concentration of the plating salt in the bath to the concentration of the same salt in the last rinse tank) the formulations were:

$R=\left ( 1+A \right )^{n}$ (parallel rinse tanks) (12)

where A is the ratio qt/θ, which, when you are thinking of returning the effluent to the plating tank, becomes E/nθ, where n is the number of rinse tanks in parallel. The value of R for series rinse tanks, which to the best of my knowledge was first published in 1952,⁵ is:

$R=1+A+A^{2}+A^{3}........+A^{n}$ (13)

or in closed form

$R=\left ( A^{n-1}-1 \right )/\left ( A-1 \right )$ (14)

All of these dragout and rinsing equations were derived on the basis of assumed perfect or instantaneous mixing in the tanks. Obviously this can't be true, yet the simplified rinsing equations based on this incorrect assumption very often gave results that were quite close to experimentally measured results, and I was puzzled about it. In the past, a number of other investigators have attempted to come up with equations closer to the truth, based on the use of Fick's Diffusion Law and the Navier-Stokes Hydrodynamic Flow Law, but ended up bogged down in a mathematical morass. Essentially all that could be obtained that way was an equation which gave a result based on pure diffusion, with no account being taken of forced convection. From the practical standpoint this was of little value. One day in the early sixties, when I was an engineering professor at the University of Evansville, I was teaching a course in heat transfer and the analogy between heat transfer and mass transfer as applied to dragout tanks and rinsing suddenly struck me.

Consider Fig. 5. A very small hot body is put into thermal contact with a much larger cool body in a perfectly insulated chamber. As shown by the temperature time curves, both bodies reach an equilibrium value T_eq. The driving force that produces the heat flux depends on the temperature difference, but how quickly both bodies arrive at the same temperature will depend also on the amount of area of the cool body in contact with the hot body. The more area in contact, the sooner will the cooler body reach the equilibrium temperature.

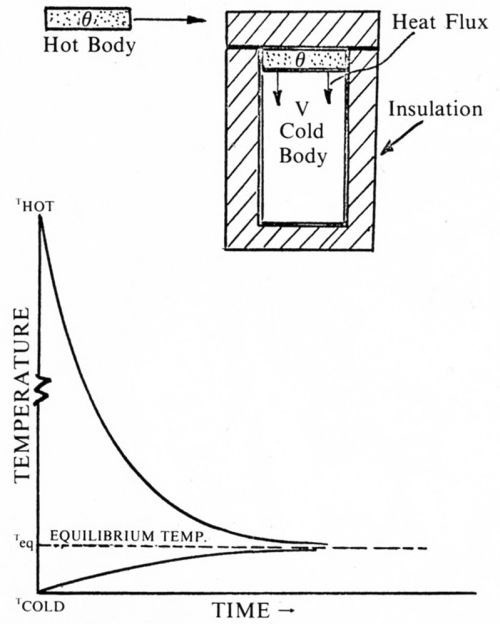
Figure 5 - Heat transfer analogy for stagnant rinsing.

Tank in tank model

Based on this idea, I invented a new model for rinsing, which is illustrated in its simplest form for a stagnant rinse tank in Fig. 6. I call this model "the tank in tank" model⁶ for rinsing. It was developed in 1964 but was not published until it appeared in my book, Water and Waste Control for the Plating Shop, in 1976. Basically, the work to be rinsed is assumed to be a closed, tiny tank or barrel containing the dragout. It is connected by an inlet pipe to an imaginary pump in the rinse tank which pumps the rinse water into the tiny tank, forcing an equal volume of liquid out of the tank at the exit pipe. Because the tiny tank is so small, the mixing inside of it can be taken to be perfect. In the past, all water running into a rinse tank was assumed to come into contact with the dragout. In this model, only the water that is pumped into the little tank comes into contact with the dragout. The rate at which the water moves into the tiny tank is designated by k (liters per unit time), which is the actual or true mixing rate for this case. The energy for operating this imaginary pump comes from the free energy difference between the concentrated dragout and the dilute rinsing solution when there is no agitation of any kind. When there is agitation, such as by water flow or air, etc., this is the energy source for the pump. Any external mixing energy that is put in goes to increasing the capacity of the imaginary pump. Increasing the capacity of this pump can be likened to increasing the heat transfer surface between the hot and cold bodies in Fig. 5.

Figure 6 - Rinsing equation (tank in tank). Case 1: Stagnant tank.

When very little mixing energy is applied, diffusion is the primary mechanism and equilibrium is reached only after a very long time, perhaps as long as fifteen minutes. Also note that the work (or tiny tank), when removed from the rinse tank, has a higher concentration of salts than that in the rinse tank. As the rate of mixing is increased, the concentration of the solution in the tiny tank drops more rapidly, and the concentration in the rinse tank increases more rapidly until they are both at about the same concentration in just a few seconds. Indeed, with a further increase in mixing energy, it is almost possible to reach the ideal of perfect or instantaneous mixing, which was the basic assumption of all the models previously discussed. The following example shows that only a relatively small amount of mixing energy is required to obtain practically perfect mixing. For this reason (except perhaps only in barrel plating), the original simple rinsing equations work quite well.

Recall the formula (1) for the concentration of solution in a single dragout tank after n rinsing cycles and let us see what happens under the following circumstances: Gold concentration, C_p, 2 g/L (2000 ppm); dragout, 0.01 liter per cycle; V, the volume of the dragout tank, 20 liters; n = 100 cycles; t, the time each item is in the rinse tank is 15 sec; k, the true mixing rate (Methods for determining k can be found in Ref. 6.) is 0.001 L/min (very poor mixing, equivalent to diffusion only). The formula for imperfect mixing, according to the "tank in tank" model is:

$C=C_{p}\left [ 1-\left ( \frac{1+\left ( \theta /V \right )exp\left ( -kt/\theta \right )}{1+\theta /V} \right )^{n} \right ]$ (15)

Accordingly $C=2000\left [ 1-\left ( \frac{1+0.0005exp\left ( -0.025 \right )}{1.0005} \right )^{100} \right ]$ = 2.46 ppm in the recovery tank.

With perfect mixing (k = infinity), formula (15) becomes formula (1)

$C=C_{p}\left ( 1-\left [ 1/\left ( 1+\theta /V \right )^{n} \right ] \right )$

and C = 2000 (1 - (1 / 1.0005)¹⁰⁰) = 97.5 ppm!

Consider the effect of more mixing energy. Taking k to equal 1.0 L/min (this is still a low mixing rate, about 15 gal/hr in more familiar terms).

$C=2000\left [ 1-\left ( \frac{1+0.0005exp\left ( -25 \right )}{1.0005} \right )^{100} \right ]$ ≈ 97.5 ppm!

This is a very important formula for those trying to recover gold or other precious metals, as it points up the value of very vigorous agitation in dragout tanks and slow flowing rinse tanks.

Coming back to rinsing with running water, a more advanced form of the tank in tank model⁶ gives the following result for the equilibrium concentration in a single rinse tank:

$C_{t}=C_{p}/\left ( 1+q/\theta +q/k \right )$ (16)

where C_t is the equilibrium concentration in the rinse tank, k is the true mixing rate in liters per unit time, q is the number of liters of water flowing into the rinse tank per unit time, θ as before is the dragout in liters flowing into the tank per unit time. The equilibrium concentration of plating salts on the rack as removed from the rinse tank is given by C_r

$C_{r}=C_{p}\left ( 1+q/k \right )/\left ( 1+q/k+q/\gamma \theta \right )$ (17)

where all symbols have the meaning given them previously.

The concentration on the rack is always higher than that in the rinse tank, and, as k becomes large as compared to q, C_r becomes approximately equal to C_t and the formulas revert to formula (10) - the one that assumed perfect mixing. Also of interest is the fact that with imperfect mixing, the average concentration in the rinse tank will be below that to be expected for perfect mixing. This is illustrated in Fig. 7.

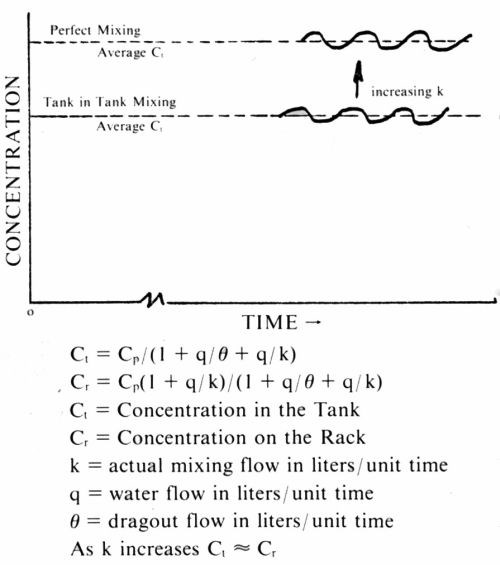
Figure 7 - Rinsing: new model (imperfect mixing).

As water flow rates go down to conserve water and reduce pollution handling costs and natural recycling⁷ becomes more popular, the true mixing rate, k, becomes more and more important. A simple example illustrates this. For three rinse tanks (parallel fed) after a chromium plating bath, the dragout rate is 0.1 L/hr, the evaporation rate is 2 L/hr with perfect mixing (k = infinity). What is R? Using formula (12), R = (1 + 20)³ = 9261, so that there is a dilution of over 9000 to 1.

With poor mixing and n parallel feed rinse tanks, the formulation for the rinsing criterion at the n^th rinse tank is:⁶

$R_{nt}=\left ( 1+q/k \right )\left [ \left ( 1+q/k+q/\theta \right )/\left ( 1+q/k \right ) \right ]^{n}$ (18)

If the mixing is poor (k = 0.1 L/ hr) with a water flow to each tank of 2 L/hr as before, the result is:

R_nt = (1 + 20) [(1 + 20 + 20) / (1 + 20)]³= 156!

If k is increased to 240 L/hr (about 4 gal/min), R_nt becomes 9120, which is just about the perfect mixing result. Accordingly, if one bears in mind that if water flow rates are reduced, the mixing rate must be strongly increased, it is possible to get the equivalent of perfect mixing without too much difficulty. The formula likewise indicates that the ratio of evaporation to dragout rate is also of great importance in the planning of systems which will return the plating solution back to the plating tank where it belongs.

Practical applications

While the mathematics and ideas discussed here may not be 100 per cent accurate, they are close enough to the truth to give anyone interested in doing so the capability of designing plating systems that keep the common pollutants out of the waterways. With proper planning, there is no need to go into large scale chemical treatment, waste and sludge processing. It can be done successfully at relatively low cost, if one is willing to try it.

Dragout is the main source of plating pollution. There are many ways not gone into here for reducing it, such as blowing it off at the plating tank, use of drip rods and fog rinses as the work leaves the tank, etc. Whatever does leave the plating tank can be returned by the use of flowing dragout tanks. Allowances can be made for the buildup of impurities by putting the returning rinse water through a purification process, which may involve carbon filtration, reduction or oxidation by electrolysis, and other standard procedures. The recycling may be done in a natural way⁷ if the evaporation rate of the plating tank sufficiently exceeds the dragout rate; if not, evaporation methods may be used to either decrease the amount of rinse water, or plating bath, to permit the return of the rinse water. The technology involved, the mathematics, the design of good rinse tanks are available to everyone, so if you don't want to offend the EPA, don't pass your plating rinse water into the sewer!

References

1. Joseph B. Kushner, Metal Industry, 33, 14 (January 1935).

2. Joseph B. Kushner, AES Monthly Review, 29, 751 (September 1942).

3. Joseph B. Kushner, Plating, 36, 798 (August 1949).

4. Joseph B. Kushner, Metal Finishing, 47, 52 (December 1949).

5. Joseph B. Kushner, Metal Finishing, 50, 60 (January 1952).

6. Joseph B. Kushner, Water & Waste Control for the Plating Shop, Cincinnati, OH, Gardner Publications, 1976.

7. Joseph B. Kushner, Metal Finishing, 69, 36 (July 1971) and (August 1971).

About the author:

This piece was written at the time Dr. Kushner was announced as the recipient of the 1976 Scientific Achievement Award:

Joseph B. Kushner is the choice of the AES Scientific Achievement Selection Committee to be the 1976 recipient of the Society's coveted award. The announcement was made at the opening session of the 63rd Annual Technical Conference of the American Electroplaters' Society in Denver, Colorado, on June 28, 1976.

A native of New York City, Dr. Kushner received a degree in chemical engineering from the Cooper Union Institute of Technology, and did graduate work in chemical engineering at Brooklyn Polytechnic Institute. He received a master's degree in metallurgical engineering from Lehigh University in 1953 and a doctorate in 1957.

Graduating, as he did, from Cooper at the height of the great depression, Dr. Kushner was fortunate to obtain a job as a plater's helper in a local costume jewelry house. This led to his interest in plating, and particularly in gold plating. In 1936, he joined AES and, the same year, accepted a post as electrochemist for A. Robinson and Son, a precious metal refining concern. In that capacity he developed "Robinson's Assayed Gold Plating Solutions," the forerunner of the modern gold plating formulation business. He was also granted several patents, one of which was for a method and solution for gold plating stainless steels, and developed the first selenium rectifier for industrial gold plating applications. The latter subsequently became the foundation upon which Green Electric Co., a firm specializing in rectifiers for plating applications, was built.

Though he would go on to other things, Dr. Kushner never lost his interest in gold plating. For example, in 1940 he began a series of articles on "Modern Gold Plating" which ran in Products Finishing until the end of 1942. These became the gold plater's bible of that day. In 1950, while acting as a consultant to a well-known Swiss watchcase manufacturer, he proposed a gold plating solution involving a chelating agent. This was later developed, patented by the company and then sold to a major supplier to become a standard plating solution for heavy gold deposition.

In 1939, Dr. Kushner went into business for himself as a plating consultant in New York City. To give job platers in the area troubleshooting help quickly, he devised a portable, miniature chemical laboratory.

After the attack on Pearl Harbor, Dr. Kushner volunteered for naval service, but was rejected because of his eyesight. He then turned to consulting, working on the development of high speed wire and small parts plating machines in connection with the war effort. From 1943-45 he accepted a position as senior electrochemical engineer working on the Manhattan District Project (SAM Laboratories at Columbia University) where he invented and patented several electrochemical processes which were assigned to the Atomic Energy Commission. He was awarded a bronze medallion by the university for his services to the project.

An active member of AES New York Branch since 1936, Dr. Kushner recognized electroplaters' need for scientific training presented in an easily assimilated form. To fill this void, he began work on a home study course, Electroplating Know How, which was completed and copyrighted in 1948. With it Dr. Kushner has trained, and continues to train, AES members and other industry personnel. In fact, many well-known AES personalities have studied with him at one time or another. In 1970, he embarked upon a comprehensive updating of the course, adding considerable new material, and the revised text, Electroplating Know How II, was published four years later.

In 1945, Dr. Kushner and his family moved to Stroudsburg, Pa., which served as the base for his consulting activities, and for the correspondence course which his wife managed. The move enabled him to complete the work on his Ph.D. at Lehigh in nearby Bethlehem. His doctorate in hand, Dr. Kushner taught at Lehigh as a visiting instructor in electrometallurgy, replacing Prof. Allison Butts. The following year, he accepted a post as associate professor of engineering at the University of Evansville, Evansville, Ind., and relocated to that area. A year later he was appointed a full professor.

Dr. Kushner has conducted considerable research in the fields of dragout, rinsing and recovery of plating effluents. His first paper, "Losses from Recovery Rinse Tanks," published in the January, 1935 issue of Metal Industry (now Metal Finishing), contained perhaps the first mathematical analysis of dragout. A later paper, "Drag-in," won an AES honorable mention and appeared in the Monthly Review of the AES, 26, 937 (1942. It provided the first scientific analysis of the way in which impurities build up in plating and rinsing tanks under certain operational conditions. With these two important papers, he quantified the problem of drag-in. In 1951, in connection with his work on rinsing and dragout problems, Dr. Kushner developed a simple instrument for measuring surface tension of plating baths. In 1949, he published an analysis of the rinsing operation in Plating (now Plating and Surface Finishing), suggesting such blue-sky notions as "long distance" and "chemical rinsing." He was also the first to develop the correct equation for equilibrium cascade (series) rinsing, publishing it in 1952. In a recent book, Water & Waste Control for the Plating Shop, he has proposed a new, improved rinsing equation which covers rinsing plating barrels and other items normally difficult to rinse.

Residual stress in electrodeposited metals has always been an intriguing subject in Dr. Kushner's opinion. In 1953, while working toward his master's degree, he invented and later patented a new instrument for measuring plating stresses based on the deflection of a disc. His doctoral dissertation was based on the use of this instrument. The recipient of two NSF Basic Research Grants, he subsequently did considerable research on stress using both his first invention and another far more sensitive instrument that he had developed for the purpose. This work indicated that at the very beginning of plating even tensile deposits may be in compressive stress; that the finer the grain size of the basis metal, the higher the maximum stress in the deposit and that with a coarser grain size, the maximum is smaller and farther away from the interface. These findings were corroborated by Armyanov and Weil.

In 1966-67, Dr. Kushner was awarded a Senior Visiting Fellowship by the British Science Council to the Department of Industrial Metallurgy at the University of Birmingham, England, where he worked with Dr. Peter Farr on the effect of hydrogen electrodeposition on palladium and palladium-silver alloys. Two papers, one published in Nature and the other in the Review of Scientific Instruments, resulted from this work. In the summer of 1968, he worked with Dr. Peter Baeyens in the electroplating laboratory at the Philips Co., Eindhoven, Holland, on gold plating solutions for PC boards and magnetic alloy plating for computer applications. The following summer, under an NSF Grant, he worked in the Department of Metallurgy at Cambridge University with Dr. T. Hoare on the electropolishing of thin metal specimens for electron microscope viewing. In addition, he did NSF-sponsored metallurgical research at Stanford University.

Beyond his correspondence course, Dr. Kushner is the author of more than 70 papers on metal finishing. He is also author of the chapter on stress in the Electroplaters' Process Control Handbook, 2^nd Ed., the chapter on rinsing and drying in Surface Preparation and Finishes for Metals, and the section on rinsing techniques in the Metal Finishing Guidebook - as well as the two volumes mentioned previously.

In addition to the American Electroplaters' Society, Dr. Kushner is a member of the Electrochemical Society, the American Society for Metals, the American Institute of Mining & Metallurgical Engineers, the American Society for Engineering Education and Sigma Xi.